Online-Puzzlespiele
Shikaku-Beispiel mit ausgearbeiteter Lösung:
 |
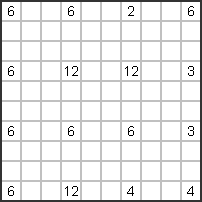
Das rechte Beispiel wollen wir nun gemeinsam lösen. Dies ist sicherlich nicht das schwierigste Rätsel. Hier geht es lediglich darum, zu zeigen, wie man tatsächlich an die Lösung eines Sikaku-Rätsels herangeht Ansätze. | |
 |
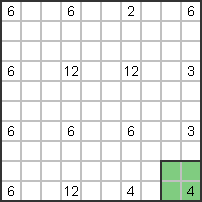
Beginnen wir in der unteren rechten Ecke. Die 4 Kästchen dürfen nicht horizontal sein Bilden Sie immer noch eine vertikale 4er-Reihe, also müssen sie ein 2x2-Quadrat bilden. | |
 |
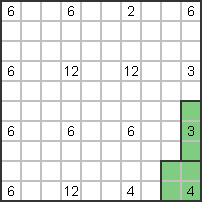
Der 3. unten rechts über dem 4. muss senkrecht und lückenlos an den 4. anschließen, da das Kästchen unter der 3 durch kein anderes Rechteck abgedeckt werden kann. Die 3 ist also vertikal. | |
 |
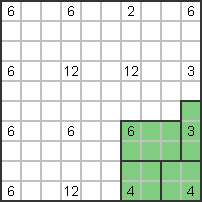
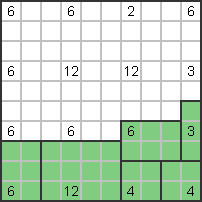
Die Zahl 6 neben der Zahl 3 rechts muss horizontal sein (3x2); die 4er Serie unten Bilden Sie ein 2x2-Quadrat. | |
 |
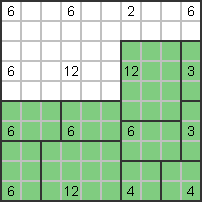
Die Zahl 12 daneben muss horizontal sein (3x4), die Zahl 6 unten links muss vertikal sein Ständer (3x2). | |
 |
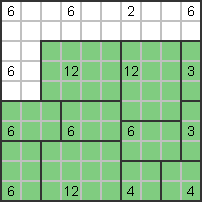
Die unteren beiden 6er müssen horizontal sein (3x2). Die Zahl 3 rechts muss vertikal stehen Ständer (3x1) und die rechten 12 müssen in der unteren rechten Ecke anliegen: | |
 |
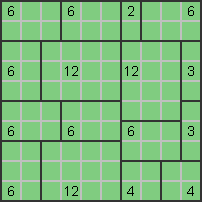
Für die restlichen 12 gibt es nur eine Option: | |
 |
Der Rest erledigt sich von selbst. |