Online Puzzle Games
Shikaku example with worked out solution:
 |
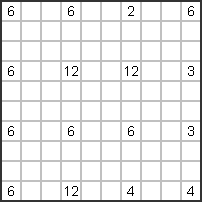
We now want to solve the example on the right together. This is certainly not the most difficult puzzle. The point here is just to show how one actually approaches solving a Sikaku puzzle approaches. | |
 |
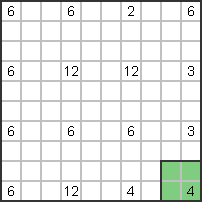
Let's start in the bottom right corner. The 4 boxes cannot be horizontal still form a vertical row of 4, so they have to form a 2x2 square. | |
 |
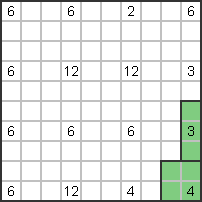
The 3rd bottom right above the 4th must connect vertically to the 4th without any gaps, since the box under the 3 cannot be covered by any other rectangle. So the 3 is vertical. | |
 |
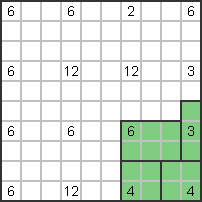
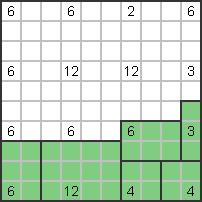
The number 6 next to the number 3 on the right must be horizontal (3x2); the 4 series below Form a 2x2 square. | |
 |
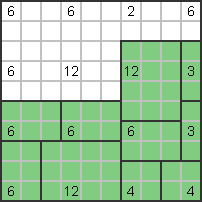
The number 12 next to it must be horizontal (3x4), the number 6 at the bottom left must be vertical stand (3x2) | |
 |
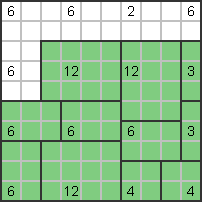
The bottom two 6s must be horizontal (3x2). The number 3 on the right must be vertical stand (3x1) and the right 12 must nestle in the bottom right corner: | |
 |
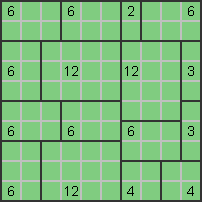
For the remaining 12 there is only one option: | |
 |
The rest takes care of itself. |