Gry Logiczne Online
Przykład Shikaku z opracowanym rozwiązaniem:
 |
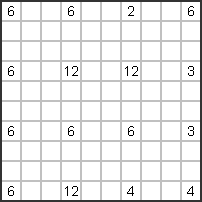
Chcemy teraz wspólnie rozwiązać przykład po prawej stronie. Z pewnością nie jest to najtrudniejsza zagadka. Chodzi tu tylko o pokazanie, jak faktycznie podchodzi się do rozwiązywania łamigłówki Sikaku podchodzi. | |
 |
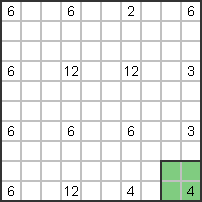
Zacznijmy od prawego dolnego rogu. 4 pola nie mogą być poziome nadal tworzą pionowy rząd 4, więc muszą utworzyć kwadrat 2x2. | |
 |
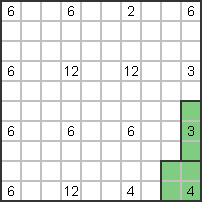
Trzeci dolny prawy nad czwartym musi łączyć się pionowo z czwartym bez żadnych przerw, ponieważ pola pod liczbą 3 nie można przykryć żadnym innym prostokątem. Zatem 3 jest pionowe. | |
 |
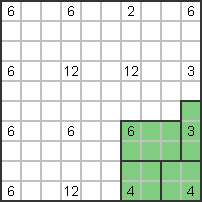
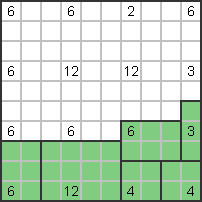
Liczba 6 obok cyfry 3 po prawej stronie musi być pozioma (3x2); 4 serie poniżej Uformuj kwadrat 2x2. | |
 |
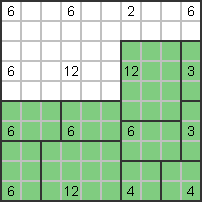
Liczba 12 obok musi być pozioma (3x4), cyfra 6 w lewym dolnym rogu musi być pionowa stojak (3x2) | |
 |
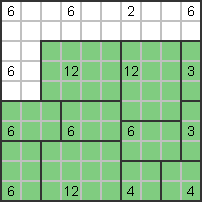
Dwie dolne szóstki muszą być poziome (3x2). Cyfra 3 po prawej stronie musi być ustawiona pionowo stojak (3x1), a prawe 12 musi znajdować się w prawym dolnym rogu: | |
 |
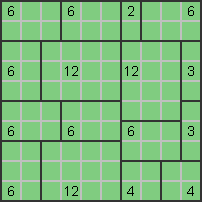
W przypadku pozostałych 12 istnieje tylko jedna opcja: | |
 |
Reszta załatwia się sama. |